Rangkuman Struktur Data 6
0AVL TREE
AVL Tree adalah BST yang memiliki perbedaan level maksimal 1 antara subtree kiri dan subtree kanan. AVL Tree berfungsi untuk menyeimbangkan(balance) BST. Dengan adanya AVL Tree, waktu pencarian dapat dipersingkat dan bentuk tree dapat disederhanakan.
Contoh AVL Tree:
Insertion dalam AVL Tree
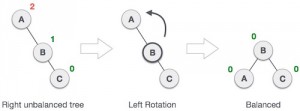
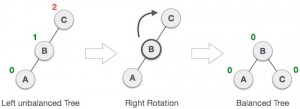
Setiap penambahan sebuah node ke AVL Tree harus dilakukan pemeriksaan dari node baru ke root. Node pertama yang memiliki balance factor lebih dari 1 diseimbangkan. Proses penyeimbangan dibagi menjadi 2, yaitu Single Rotation dan Double Rotation.
Single Rotation
- Left Rotation
- Right Rotation
Double Rotation
- Left-Right Rotation
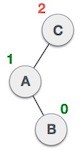 Sebuah node dimasukkan ke subtree kanan dari subtree kiri.
Sebuah node dimasukkan ke subtree kanan dari subtree kiri.
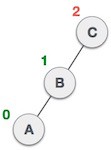
 Lakukan left rotation pada subtree kiri dari node C. A menjadi subtree kiri dari B.
Lakukan left rotation pada subtree kiri dari node C. A menjadi subtree kiri dari B.
 Node C masih belum seimbang karena subtree kiri dari subtree kiri.
Node C masih belum seimbang karena subtree kiri dari subtree kiri.
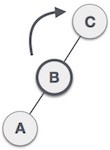 Lakukan right rotation sehingga B menjadi root, C menjadi subtree kanan dari subtree kirinya.
Lakukan right rotation sehingga B menjadi root, C menjadi subtree kanan dari subtree kirinya.
- Right-Left Rotation
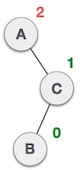 Sebuah node dimasukkan ke subtree kiri dari subtree kanan.
Sebuah node dimasukkan ke subtree kiri dari subtree kanan.
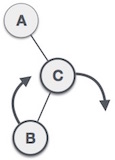 Lakukan right rotation pada node C. C menjadi subtree kanan dari subtree kirinya. B menjadi subtree kanan dari A.
Lakukan right rotation pada node C. C menjadi subtree kanan dari subtree kirinya. B menjadi subtree kanan dari A.
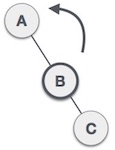 Lakukan left rotation sehingga B menjadi root, A menjadi subtree kiri dari subtree kanan nya.
Lakukan left rotation sehingga B menjadi root, A menjadi subtree kiri dari subtree kanan nya.
Deletion dalam AVL Tree
Deletion dalam AVL Tree mirip dengan BST, hanya perlu diperhatikan keseimbangan tree seperti dalam insertion. Lakukan single atau double rotation setiap ada ketidakseimbangan.
GUEST LECTURE
Guest lecture: Selvakumar Manickam dari University of Science, Malaysia.
Guest lecture menjelaskan tentang Tree, BST, serta keektifannya.
Rangkuman Struktur Data 5
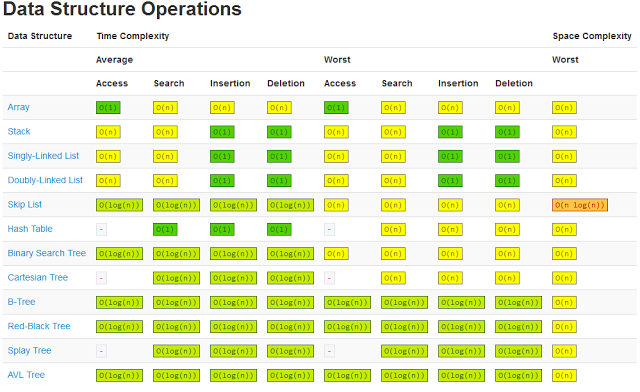
0BINARY SEARCH TREE
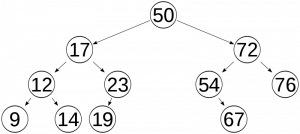
Binary Search Tree (BST) adalah binary tree dimana sub tree sebelah kiri lebih kecil daripada parentnya.
Data pada BST sudah terurut sehingga mempermudah dalam proses pencarian.
Operasi-operasi dalam BST:
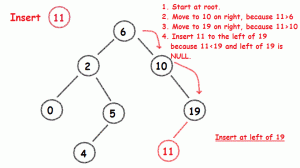
1. Insert
Memasukkan data ke dalam BST. Data yang dimasukkan akan menjadi leaf.
Penempatan data yang dimasukkan akan mengikuti sifat BST, jika data lebih kecil dari parent maka akan ke kiri, jika lebih besar maka akan ke kanan, seterusnya hingga menempati posisi leaf.
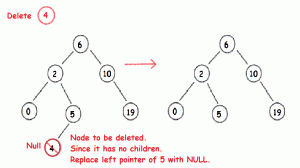
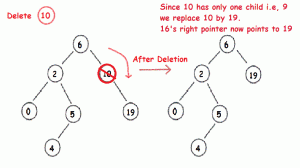
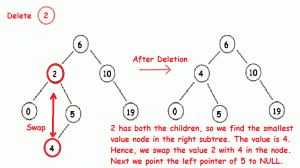
2. Delete
Menghapus data dalam BST.
- Jika yang dihapus tidak mempunyai anak (leaf) , maka langsung hapus data tersebut
- Jika yang dihapus mempunyai 1 anak, maka data dihapus, lalu sambungkan anak dari node yang dihapus dengan parent dari node tersebut.
- Jika yang dihapus mempunyai 2 anak, digantikan oleh data paling kiri dari subtree kanan, atau sebaliknya.
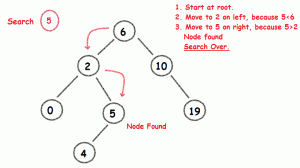
3. Search
Digunakan untuk mencari data dalam BST.
Step-stepnya:
– Dimulai dari root
– Jika data yang dicari sama dengan node, maka pencarian berakhir.
– Jika data lebih kecil dari node, maka:
- Jika node mempunyai subtree kiri, maka lanjutkan pencarian ke subtree kiri
- Jika tidak punya subtree kiri, pencarian berakhir, pencarian gagal.
– Jika data lebih besar dari node, maka:
- Jika node mempunyai subtree kanan, maka lanjutkan pencarian ke subtree kanan
- Jika tidak punya subtree kanan, maka pencarian berakhir, pencarian gagal.
– Ulangi step diatas sampai menemukan node yang dicari.
Rangkuman Struktur Data 4
0TREE
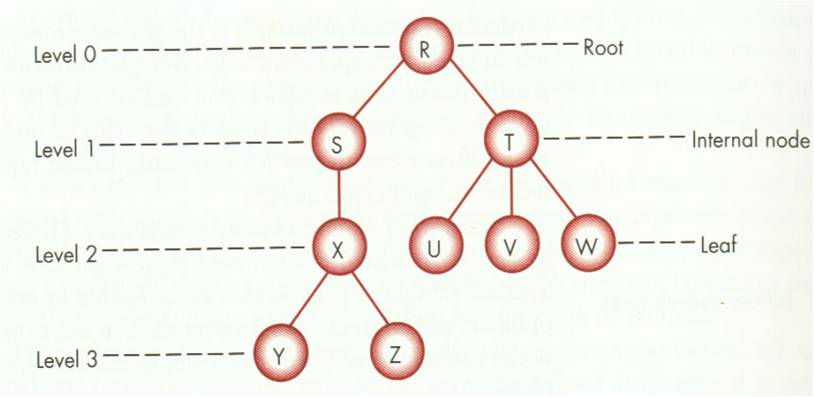
Tree adalah sebuah struktur data yang berbentuk seperti pohon yang terdiri dari serangkaian node yang saling berhubungan.
Root adalah node teratas dari sebuah tree.
Parent adalah node yang berada diatas node lain secara langsung. Root juga termasuk parent.
Child/anak adalah cabang langsung dari sebuah node.
Leaf/Daun adalah node terakhir yang tidak memiliki child.
Derajat adalah tingkatan dalam tree, dimulai dari level 0 untuk root dan level 1 untuk child dibawahnya dan seterusnya.
Height adalah banyaknya tingkatan dalam suatu tree.
Size adalah banyaknya node dalam suatu tree.
Ancestor adalah seluruh node yang terletak sebelum node tertentu pada jalur yang sama.
Descendant adalah seluruh node yang terletak setelah node tertentu pada jalur yang sama.
Sibling adalah node-node yang memiliki parent yang sama.
BINARY TREE
Binary Tree adalah tree yang mempunyai maksimal hanya dua anak dan harus terpisah.
Tipe-tipe Binary Tree:
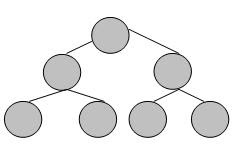
- Perfect Binary Tree : masing-masing node mempunyai dua anak.
- Complete Binary Tree : mirip dengan Perfect, tetapi setiap subtree boleh memiliki panjang path yang berbeda.
- Skewed Binary Tree : masing-masing node kecuali leaf hanya mempunyai satu anak.
- Balance Binary Tree : jarak dari root ke leave dibagian kiri dan kanan sama.
PROPERTY OF BINARY TREE
Jumlah max node dari level k dari sebuah binary tree adalah 2k
Jumlah max node dengan height h dari sebuah binary tree adalah 2h+1-1
Height minimum dari sebuah binary tree dari n node adalah 2logn
Height maksimum dari sebuah binary tree dari n node adalah n-1
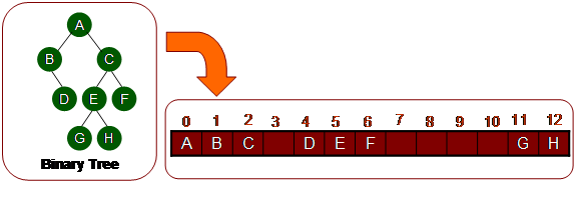
REPRESENTATION OF BINARY TREE
- ARRAY
Index pada array mewakili jumlah node
Index 0 adalah Root
Index Left Child = 2p + 1, dimana p = parent index
Index Right Child = 2p + 2
Index Parent = (p-1)/2
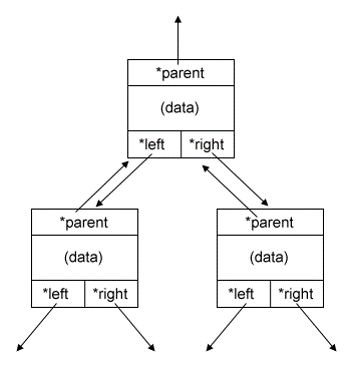
- LINKED LIST
struct node {
int data;
struct node *left;
struct node *right;
struct node *parent;
};
struct node *root = NULL;
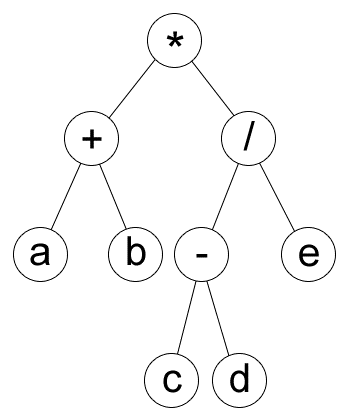
EXPRESSION TREE CONCEPT
PREFIX : print L R
Atas ke bawah, dengan kiri prioritas
*
*+
*+a
*+ab
*+ab/
*+ab/-
*+ab/-c
*+ab/-cd
*+ab/-cde
POSTFIX : L R print
Kiri ke kanan, atas ke bawah
a
ab
ab+
ab+c
ab+cd
ab+cd-
ab+cd-e
ab+cd-e/
ab+cd-e/*
INFIX : L print R
Bawah ke atas, kiri ke kanan
(a
(a+
(a+b)
(a+b)*
(a+b)*((c
(a+b)*((c-
(a+b)*((c-d)
(a+b)*((c-d)/
(a+b)*((c-d)/e)

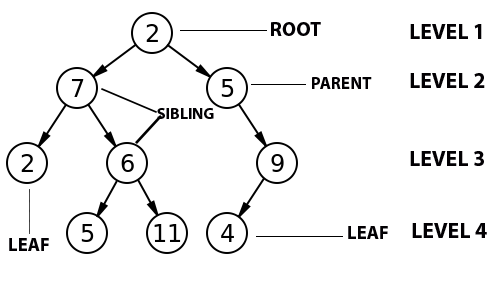
Recent Comments